O,G,H分别是△ABC的外心,重心,垂心,求证:O,G,H三点共线
 此主题相关图片如下:
此主题相关图片如下: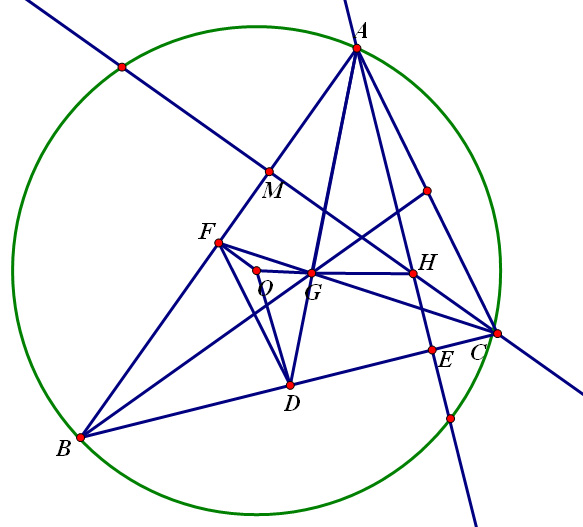
转自网络:这条线有名称~叫 欧拉线~
设H,G,O,分别为△ABC的垂心、重心、外心
。连接AG并延长交BC于D, 则可知D为BC中点。 连接OD ,又因为O为外心,所以OD⊥BC。连接AH并延长交BC于E,因H为垂心,所以 AE⊥BC。所以OD//AE,有∠ODA=∠EAD。由于G为重心,则GA:GD=2:1。 连接CG并延长交BA于F,则可知F为AB中点。同理,OF//CM.所以有∠OFC=∠MCF 连接FD,有FD平行AC,且有DF:AC=1:2。FD平行AC,所以∠DFC=∠FCA,∠FDA=∠CAD,又∠OFC=∠MCF,∠ODA=∠EAD,相减可得∠OFD=∠HCA,∠ODF=∠EAC,所以有△OFD∽△HCA,所以OD:HA=DF:AC=1:2;又GA:GD=2:1所以OD:HA=GA:GD=2:1 又∠ODA=∠EAD,所以△OGD∽△HGA。所以∠OGD=∠AGH,又连接AG并延长,所以∠AGH+∠DGH=180°,所以∠OGD+∠DGH=180°。即O、G、H三点共线。