此主题相关图片如下:
此主题相关图片如下: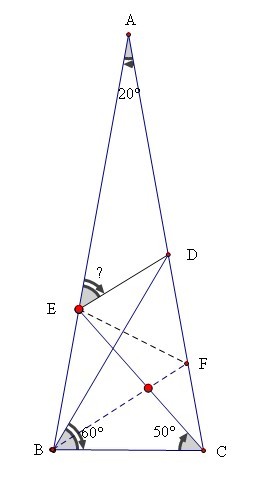
∠DBC=60°,∠ECB=50°,∴∠ABD=20°,∠ACE=30°
在△BEC中
∠BEC=180°-∠ABC-∠ECB
=180°-80°-50 =50°=∠ECB
∴BC=BE
在△BDC中
∠BDC=180°-∠DCB-∠DBC
=180°-80°-60° =40°
过B作BF=BC,BF交AC于F,则△BFC是等腰三角形
∴BF=BC=BE
又∠CBF=180°-2∠ACB=20°,∴∠FBE=80°-20°=60°
∴△BEF是等边三角形,∴BF=EF;∠BEF=60°
在△BFD中,∠FBD=∠ABC-∠ABD-∠CBF=80°-20°-20°=40°=∠FDB 故DF=BF=EF,
∴△DEF是等腰三角形
由∠DFE=180°-∠BFC-∠BFE=180°-80°-60°=40°
知∠DEF=1/2(180°-∠DFE)=70°
∴∠AED=180°-∠DEF-∠BEF=180-70°-60°=50°